Lens Formula Class 10: Lenses play a crucial role in the formation of images in the field of optics. Various devices including cameras, telescopes, microscopes, and eyeglasses use them frequently. For Engineers, physicists, and anybody interested in optics, it is essential to understand how lenses behave and form images. The lens formula is one basic equation that controls the relationship between object distance, image distance, and focal length. The lens formula is expressed as 1/f = 1/v – 1/u.
In this formula, the focal length of the lens is represented by “f,” the image distance is represented by “v,” and the object distance is represented by “u.” The object distance (u) signifies the separation between the object and the lens, whereas the image distance (v) denotes the separation between the lens and the image produced by it. The focal length (f) of a lens measures its capability to either converge or diverge light rays.
This article will explain lens maker formula derivation, magnification formula for the lens, power of lens formula, mirror formula, and other information.
Lens Maker Formula Derivation:
For various optical instruments, lenses with different focal lengths are utilized. The focal length of the lenses depends upon the radii of curvatures of the two surfaces and the refractive index of the material of the lens. To help applicants better understand the concept, the lens maker formula’s derivation is provided here. Manufacturers of lenses frequently utilize the lens maker formula to create lenses with the specified focal length. In deriving the lens maker formula, we make the following assumptions.
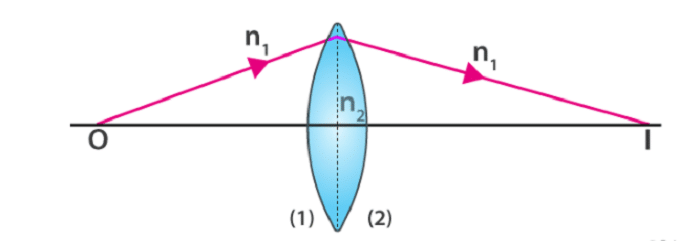
- Consider the thin lens with two refracting surfaces that have corresponding radii of curvature of R1 and R2 in the image above.
- Let n1 and n2 be the refractive indices of the surrounding medium and the lens material, respectively.
Derivation of Lens Maker Formula:
The lens maker formula’s complete derivation is explained below. We can say that using the formula for refraction at a single spherical surface,
For the first surface,
n2/v1 – n1/u = n2-n1/R1 ………… (1)
For the second surface,
n1/v – n2/v1 = n1-n2/R2 ………… (2)
Adding equations (1) and (2) now,
(n2/v1 – n1/u) + (n1/v – n2/v1) = (n2-n1/R1) + (n1-n2/R2).
n1/v – n1/u = (n2 – n1) [1/R1 – 1/R2].
n1( 1/v – 1/u) = (n2 – n1) [1/R1 – 1/R2]
1/v – 1/u = (n2 – n1) [1/R1 – 1/R2] / n1.
1/v – 1/u = (n2/n1 – 1) [1/R1 – 1/R2].
When u = ∞ and v = f
1/f = (n2/n1 – 1) [1/R1 – 1/R2].
But also,
1/v – 1/u = 1/f
Hence, we can say that,
1/f = (μ – 1) [1/R1 – 1/R2].
Where μ is the refractive index of the material. This is the lens maker formula derivation.
Magnification Formula For Lens:
The height of an image divided by the height of an object is known as the magnification of a lens. It is also given in terms of object distance and image distance. It is equal to the ratio of image distance to that of object distance.
In other words, the magnification formula for a lens relates the size of the image formed by the lens (height or length) to the size of the object being observed. The formula is given by:
Magnification (m) = height or length of the image (h’) / height or length of the object (h).
Ie., m = h’/h.
The magnification can also express in terms of the image distance (v) and the object distance (u) from the lens.
Magnification (m) = v/u.
Hence, Magnification (m) = h’/h = v/u.
Here, m = magnification.
h’ = height of the image.
h = height of an object.
v = image distance.
u = object distance.
The magnification formula is fundamental in understanding how lenses produce enlarged or reduced images compared to the original objects. It uses widely in optics, photography, microscopy, and other fields where lenses are employed to visualize and magnify objects.
Power Of Lens Formula:
The power of a lens is a measure of its ability to refract light that will define as the reciprocal of its focal length. The power of the lens can calculate using the following formula:
Power (P) = 1 / focal length (f).
The unit of power is diopters (D). where is equivalent to meters ^ -1.
To calculate the power of a lens, you need to know the focal length of the lens. The focal length can be positive for converging lenses (Convex) and negative for diverging lenses (Concave). The power of the converging lens is positive, indicating its ability to converge light rays, while the power of diverging lens is negative, indicating its ability to diverge light rays.
For example, if a lens has a focal length of 0.25 meters (or 25 centimeters), its power can calculate as:
Power (P) = 1 / 0.25 = 4 D
This means that the lens has a power of 4 diopters, indicating its ability to converge or diverge light.
The power of a lens is a fundamental concept in optics that will use in various applications, including eyeglasses prescriptions, contact lenses, and the design of optical systems. It provides quantitative measures of the optical properties of a lens and allows for comparisons between different lenses based on their ability to focus or diverge light.
Mirror Formula And Lens Formula:
In optics, the mirror formula and the lens formula are two equations that will use to describe the behavior of mirrors and lenses, respectively. Both formulas relate the object distance, image distance, and focal length, but they differ depending on whether the optical element is a mirror or a lens.
Mirror Formula:
To calculate the relationship between the object distance (u), the image distance (v), and the focal length (f) of a mirror using the Mirror Formula. The Mirror Formula is:
In this formula, “u” represent the object distance, which is the distance between the object and the mirror. “v” represents the image distance, which is the distance between the mirror and the image formed by the mirror. “f” represents the focal length of the mirror, which is the distance between the mirror’s surface and its focal point.
The mirror formula allows you to calculate any one of the three variables (u, v, or f) if you know the values of the other two variables. It uses commonly to analyze the formation of images by mirrors, including concave (converging) and convex (diverging) mirrors.
Lens Formula:
On the other hand, the lens formula uses to calculate the relationship between the object distance (u), the image distance (v), and the focal length (f) of a lens. The Lens Formula is:
1/f = 1/v – 1/u.
In this formula, the quantities have the same meanings as in the mirror formula. However, in the lens formula, the signs reverse when compares to the mirror formula.
Similarly to the mirror formula, the lens formula allows you to calculate any one of the three variables (u, v, and f) if you know the values of the other two variables. It uses commonly to analyze the formation of images by lenses, including converging (convex) and diverging (concave) lenses.
Both the mirror formula and lens formula are fundamental equations in optics, allowing for the analysis and calculation of image characteristics formed by mirrors and lenses. Understanding these formulas is essential for studying the behavior of light rays and the formation of images in various optical systems.